SQLのEXISTS述語で述語論理の量化を表現する

SQL

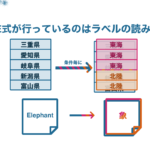
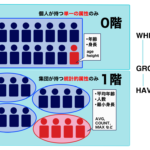
数ヶ月前に『達人に学ぶSQL徹底指南書 第2版 初級者で終わりたくないあなたへ』を読みました。EXISTSってなんとなく使われているSQLを読むことはできると思いますが、いざ自分がEXISTS述語を使用してSQLを記述できるかと言われると不安な方もいるのではないでしょうか。本書から要点を抜粋していきたいと思います。

述語論理とEXISTS述語

SQLを支える基礎理論の2つのうち、1つは集合ですがもう一つが現代の標準的な論理学である述語論理です。この述語論理において量化という重要な概念をEXISTS述語が担っています。EXISTS述語の説明の前に述語論理について理解しておきましょう。

SQLとリレーショナルデータベースを支える基礎理論は、大きく2つあります。1つが、数学の一分野である集合論。そしてもう1つが、現代論理学の標準的な体系である述語論理、正確には、少し範囲を限定した「一階述語論理」です。

達人に学ぶSQL徹底指南書 第2版 EXISTS 述語の使い方

述語とは何か

まず述語についてですが、SQLにおける述語とは何かについて、まずはChatGPTに聞いてみました。

SQLの述語（predicate）とは、SQLステートメント内で条件を指定するために使用される要素です。述語は、SQLクエリの特定の部分に対して条件を設定し、その条件が満たされる場合にのみ行を返します。述語は主に以下の構造で使用されます：

  1. WHERE句: 指定された条件を満たす行を選択するために使用されます。
  2. HAVING句: グループ化された行の条件を設定するために使用されます。
  3. JOIN句: テーブルを結合する際に、結合条件を指定するために使用されます。

どうも、SQLにおいて条件に当たる部分のことで、述語は条件に応じて行を返すということのようです。

本書で述べられているのはもっと本質的でわかりやすい説明です。
述語というのは、関数の中で戻り値が真理値になる関数のことです。だから、SQLの述語は true, false, unknown のいずれかの値を返します。冒頭に述べた通り、EXISTS句は、述語論理の量化 (quantification) と言う機能を満たすために導入された述語です。

集合と述語はほぼ同義

リレーショナルデータベースの理論において、テーブルの各行は一つの命題と見なすことができます。この命題は、その行に含まれるデータが真であることを主張します。

student_idsubjectscore
1国語55
2数学65
3英語75

このテーブルの各行は次のような命題を表します。

  • (1, ‘国語’, 55)：生徒IDが1の学生は国語で55点を取った。
  • (2, ‘数学’, 65)：生徒IDが2の学生は数学で65点を取った。
  • (3, ‘英語’, 75)：生徒IDが3の学生は英語で75点を取った。

つまり、SELECT文でWERER句を使用する場合も、WERER句で条件が真となる行を選択し、その結果真となる行をを返しているという点では、述語を組み合わせて1つの述語を戻り値として返しているといえます。述語によって命題が真となるテーブルを返しているという意味で、集合と述語はほぼ同義とみなせます。

全称量化と存在量化

では、述語論理の量化とは何かということですが、
述語論理における量化は、命題の対象となる範囲を指定するために使用されるもので、量化には「全称量化（Universal Quantification）と存在量化（Existential Quantification）の2種類があります。

全称量化（Universal Quantification）と存在量化（Existential Quantification）は、数理論理学や形式論理学において重要な概念です。

全称量化（Universal Quantification）

全称量化は、すべての対象について述べる場合に使用します。記号は ∀ で表されます。

  • 記号: ∀
  • 例: 「すべてのxに対して、P(x)が成り立つ」という命題は、∀x P(x) で表されます。
  • 意味: x の値が何であっても、P(x) が真である。

存在量化（Existential Quantification）

存在量化は、少なくとも1つの対象について述べる場合に使用します。記号は ∃ で表されます。

  • 記号: ∃
  • 例: 「あるxが存在して、P(x)が成り立つ」という命題は、∃x P(x) で表されます。
  • 意味: x の値が少なくとも1つ存在して、その値について P(x) が真である。

ド・モルガンの法則 (De Morgan’s Laws) in Quantification

ド・モルガンの法則は、述語論理の量化子に対しても適用されます。具体的には、否定の対象となる量化子を変換する方法です。
※要するに伝えたいのは、全称量化と存在量化はド・モルガンの法則という同値変形の規則を使用すれば、お互いに変換できるんだよ、というお話です。

全称量化: 全称量化は、存在量化の二重否定として表現できます。

  • 記号: ∀x P(x) ≡ ¬∃x ¬P(x)
  • 意味: 「すべてのxについてP(x)が成り立つ」という命題は、「少なくとも1つのxについてP(x)が成り立たない」という命題の否定と同等。（条件P(x)を満たさないxが存在しない）

存在量化: 存在量化は、全称量化の二重否定として表現できます。

  • 記号: ∃x P(x) ≡ ¬∀x ¬P(x)
  • 意味:
  • 「少なくとも1つの x についてP(x) が成り立つ」という命題は、「すべての x についてP(x)が成り立たない」という命題の否定と同等です。（すべてのxが条件P(x)を満たさないわけではない）

このように、述語論理の量化は、命題の範囲や対象を明確にするための重要な概念であり、論理的な証明や推論において頻繁に使用されます。

存在の階層について

ここでのポイントは、EXISTS句はその引数にスカラ値ではなく行の集合を取るという性質です。EXISTS句に限らないことですが、関数がどういう引数を取るのかは重要です。BETWEENやIN述語と違って、EXISTS句は行の集合を引数に取ります。

存在の階層については以下の記事でも触れています。

SQLのGROUP BYは集約ではなく属性の値によって切り分けるという機能を持つ
数ヶ月前に『達人に学ぶSQL徹底指南書 第2版 初級者で終わりたくないあなたへ』を読みました。GROUP BY について、業務でGROUP BYに関連した不具合があったり、切り分けるという考えの方がイメージしやすかったので、ちょっと触れてみ...
tknagayoshi.com

EXISTS述語とは何か

これまでの話をまとめると、SQLのEXISTS述語とはSQLを支える重要な理論の述語論理のうち、存在量化を実現するために導入されました。この機能があるおかげである行の集合に対して条件判断を行うことができるというわけですね。（ちなみに、SQLには全称量化がありません。）

EXISTSは複数行を一単位とみなした高度な条件を記述することができるうえ、相関サブクエリを利用するにも関わらずパフォーマンスが非常に優れるという利点があります。

達人に学ぶSQL徹底指南書 第2版 EXISTS 述語の使い方

EXISTSがのパフォーマンスが優れる理由はいくつかあるかと思いますが、「評価の早期終了」であったり、オプティマイザにおける「相関サブクエリの最適化」や「インデックスの効果的な使用」が挙げられます。

以下の書籍にも同様なことが記述されてますね。

EXISTSを使わなくてもIN(およびNOT IN)によって、ほぼ代用できる。
EXISTSの引数は常に相関サブクエリを指定する。
EXISTSの引数のサブクエリは常に「SELECT *」を使う。

SQL 第2版: ゼロからはじめるデータベース操作 EXISTS

EXISTSの引数の相関サブクエリに書くSELECT句にはその性質上、ほぼ「ワイルドカード (*)」か「1」です。当然、true or falseにか返さないので何を返しても基本的に変わらないわけですから。

EXISTS述語のサンプル

簡単なサンプルで、全称量化の命題をNOT EXISTSで表現するサンプルを見ていきます。

全称量化は存在量化の二重否定に変換する

以下のサンプルを用いて確認していきます。このテーブルから「すべての教科が70点以上である」という生徒の集合を選択します。

どういう思考で考えるかというと、各生徒ごとの集合の中でそれぞれの教科が70点以上であるかどうかを考えます。つまり、ある生徒という行の集合を入力として、その中で全てのx(教科)について70点以上という存在の有無を求められていることから、これはEXISTS述語で記述できるな、と考えられそうです。

WITH TestScores (student_id, subject, score) AS (
    SELECT 1, '国語', 55 FROM dual UNION ALL
    SELECT 1, '物理', 35 FROM dual UNION ALL
    SELECT 1, '化学', 75 FROM dual UNION ALL
    SELECT 2, '数学', 70 FROM dual UNION ALL
    SELECT 2, '国語', 60 FROM dual UNION ALL
    SELECT 2, '物理', 40 FROM dual UNION ALL
    SELECT 2, '数学', 65 FROM dual UNION ALL
    SELECT 3, '英語', 75 FROM dual UNION ALL
    SELECT 3, '数学', 70 FROM dual UNION ALL
    SELECT 4, '化学', 80 FROM dual UNION ALL
    SELECT 4, '英語', 85 FROM dual
)

全称量化の命題「すべての教科が70点以上である」を二重否定に同値変換すると存在量化を使用して「50点未満である教科が1つも存在しない」に書き換えられて、これを NOT EXISTS で表現できます。

SELECT DISTINCT student_id
FROM TestScores ts1
WHERE NOT EXISTS (
    SELECT *
    FROM TestScores ts2
    WHERE ts1.student_id = ts2.student_id
    AND ts2.score < 70 -- 70点未満の強化
);

相関サブクエリの流れをちょっと考えてみると、TestScores の各レコードに対して順にサブクエリが実行されます。で、そのサブクエリの処理としては、外側のクエリの生徒を引数のような感じでサブクエリ内の生徒でバインドして、そのスコアを確認します。

HAVING句による置き換え

個体ではなく集合レベルの条件の操作を行うという点でEXISTS句はHAVING句と置き換えられる場合が可能だったりします。HAVING句は集合に対する条件を定義します。各生徒ごとの集合の中ですべての教科が70点以上であるかどうか、つまり、各生徒ごとの集合の中で最低点数が70点以上であれば良いので、以下のようなSQLになりますね。

SELECT student_id
FROM TestScores
GROUP BY student_id
HAVING MIN(score) >= 70;

参照

達人に学ぶSQL徹底指南書 第2版 初級者で終わりたくないあなたへ
SQL 第2版 ゼロからはじめるデータベース操作

タイトルとURLをコピーしました